Can You Design The Perfect Wedding?¶
Riddler Classic¶
Rumor has it that readers of The Riddler Ellora Sarkar and Daniel Gomez are getting married this weekend. Congratulations to you both! In keeping with the hexagonal design of your wedding backdrop, I thought you might enjoy the following puzzle. (Riddler Nation, this one’s for you, too!)
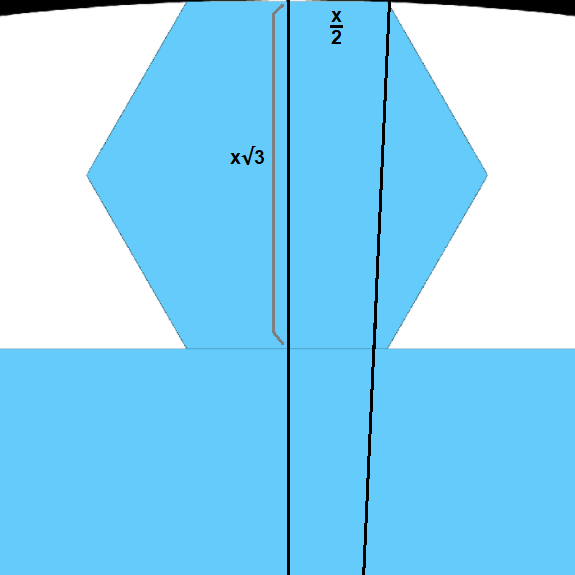
The larger regular hexagon in the diagram below has a side length of 1.

What is the side length of the smaller regular hexagon?
Extra credit: If you look very closely, there are two more, even smaller hexagons on top. Can you see them? No? Maybe this animation will help:

What are the side lengths of these two even smaller hexagons?